Es ya un tópico, pero no hay cuestión que Leonardo da Vinci parezca que no hubiera tratado, aunque fuere de forma superficial. Y, en efecto, también le interesaban los mapas. En el Codex Atlanticus, que viene a ser una especie de compendio de papeles diversos de Leonardo dispuesto en varios volúmenes y conservado en la Biblioteca Ambrosiana de Milán, aparecen esbozos de diversos tipos de proyección cartográfica. La mayoría eran conocidos en su tiempo, pero una en particular parece ser obra de Leonardo o, al menos, introdujo en ella ciertos elementos originales, aunque ha habido polémicas sobre ello (algunos autores afirman que ya se había contemplado el uso de este tipo de proyección anteriormente). El dicciónario de la RAE define un octante como:
Instrumento astronómico del tipo del quintante y del sextante, y de análoga aplicación en barcos y aviones, cuyo sector comprende solo 45 grados o la octava parte del círculo.
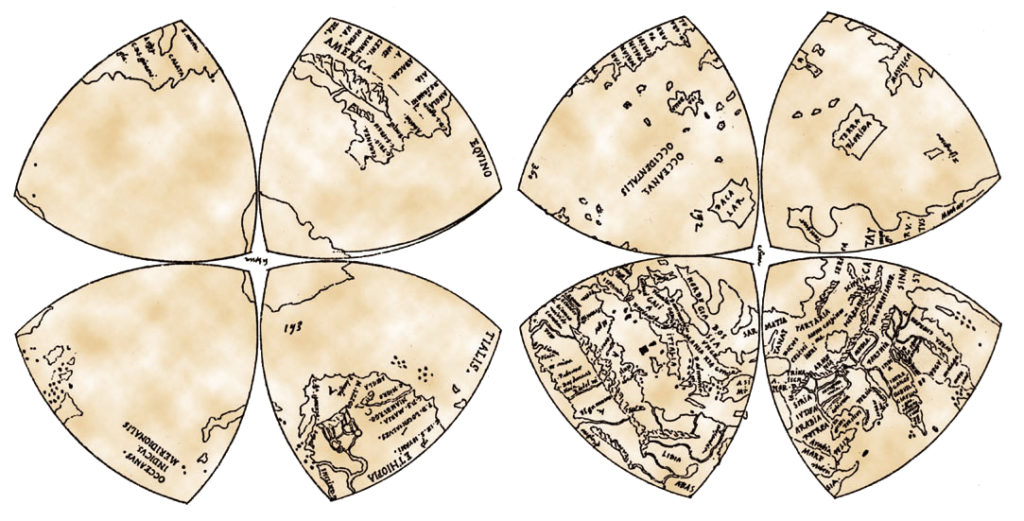
Lo menciono porque la proyección más curiosa de las utilizadas por Leonardo era, precisamente, la que es conocida como «proyección en octantes», con un esbozo inicial del año 1508 y un mapa más elaborado en 1514. Esta proyección dividía el mundo en ocho partes a modo de triángulos de Reuleaux1, como si un trébol de cuatro hojas se tratara para cada hemisferio. Como puede verse en la imagen que aparece a continuación, la esfera del globo terrestre está dividida en ocho triángulos esféricos equiláteros. Curiosamente, fue uno de los primeros mapas en los que se menciona a América por su nombre y, también, uno de los primeros en colocar la Antártida, aunque más como un caso de imaginaria «Terra Australis» que como algo real. El dibujo parece ser, según los expertos, obra de algún copista que hubiera trabajado bajo encargo del propio Leonardo.
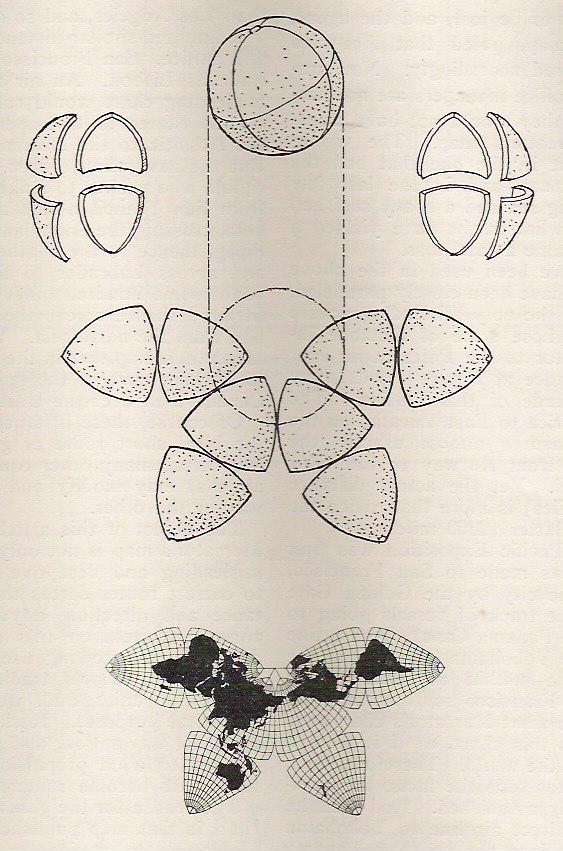
A principios del siglo XX el cartógrafo e ingeniero Joseph Stanislaus Cahill dio una vuelta de tuerca al concepto con su proyección tipo «mariposa», cuya evolución más refinada dio lugar a la proyección Cahill–Keyes.
_________________
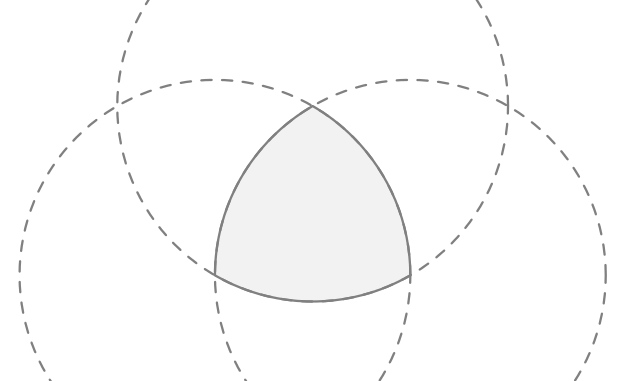
1 Es la clase más sencilla de polígonos de Reuleaux, que son aquellos que tienen la particularidad de tener curvas de anchura constante.

